Click to view the roller bearingElectric motor shafts are supported on bearings of different types. Some bearings contain rolling elements (these are ball bearings or roller bearings), while others (journal bearings) don't.
Bearings that contain rolling elements will show characteristic frequencies in the vibration spectra, which are related to the internal structure of the bearing. For example, imagine a roller bearing in which one bearing shell has a nick on its surface:
Click to view the roller bearing
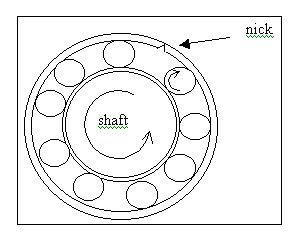
The frequency with which the balls hit the nick (and create a vibrational impulse) will be a function of the shaft rotational speed, the number of balls, and the dimensions of the balls and the bearing shells or races. There are a number of possible bearing faults.
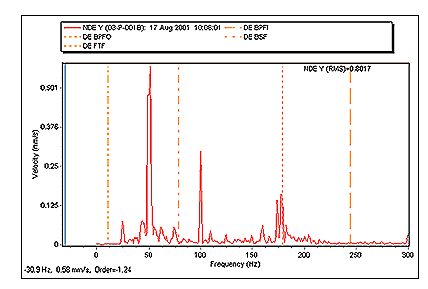
The bearing frequencies will then be calculated by our software, taking the running speed into account. In the following graph, it can be seen that there is a vibration developing at about 178Hz, which is almost certainly a defect in the fixed (or outer) bearing race (BPFO).
Click to view the bearing harmonics graph
If the bearing in your piece of machinery is not in our bearing frequency database, please let us know. So far, we have over 7000 different bearings in the database. For an unknown bearing, the frequencies produced by these faults are calculated as follows:
For a defect on the inner bearing race (BPFI, or ball pass frequency inner):
BPFI = Nb/2 x (1 + (Bd/Pd) cosq) x RPM
where Nb is the number of balls, Bd is the ball or roller diameter, Pd is the bearing pitch diameter, q is the contact angle (usually assumed to be 0°) and RPM is the speed of the motor.
For a defect on the outer race (BPFO):
BPFO = Nb/2 x (1 - (Bd/Pd) cosq) x RPM
For a defect on one of the rolling elements (BSF, or ball spin frequency):
BSF = Pd/2Bd x (1 - (Bd/Pd)2 cos2q) x RPM
For a defect in the cage holding the rolling elements (FTF or fundamental train frequency):
FTF = 1/2 x (1 - (Bd/Pd) cosq) x RPM
The bearing pitch diameter Pd is not usually given in catalogs, but can be reasonably precisely calculated (for large bearings of the type we are likely to encounter) as the average of the inner and outer race diameters:
Pd = (Di + Do)/2
In order to calculate the bearing vibration frequencies, we need to know the bearing type. Most types are standard across the major manufacturers (SKF, FAG and NSK); so that a code such as NU226E will apply to the same type of bearing from any manufacturer. Once we know the bearing code, we can look up the characteristics: Nb is the number of balls, Bd is the ball or roller diameter, Di is the inner race diameter, Do is the outer race diameter.
From this we can calculate Pd. The motor speed (RPM) we get from the tachometer reading recorded at the same time as the spectrum on display, and we will almost always assume the contact angle to be 0°. We can then calculate and plot the four defect frequencies, and display them on the graph.
Journal bearings (sometimes also called oil bearings or white metal bearings) support the rotating shaft between fixed metal shells. Wear is prevented by a thin film of oil which is maintained hydrodynamically between the moving shaft and the fixed shells. Deterioration of the bearing is visible in terms of increasing amplitudes of the running speed harmonics and will not be dealt with here. However, a phenomenon called oil whirl, in which the shaft/bearing/oil film system becomes unstable, can occur. This manifests itself as a spectral peak at a frequency between 0.4 x and 0.48 x the fundamental running frequency. In cases where a motor has a journal bearing, it would be helpful to display this frequency band.